Spacetime geometry
Spacetime geometry is a subtle synthesis of Newton and Leibniz’s views: while measurements of space and time separately are relative (Leibniz), the unified spacetime geometry has an absolute character (Newton).
- Relative (changes between reference frames):
- Time intervals (time dilation)
- Spatial distances (length contraction)
- Simultaneity of events
- Velocity measurements
- Absolute (same in all frames):
- Speed of light (c)
- Spacetime interval between events
- Laws of physics
- Causality
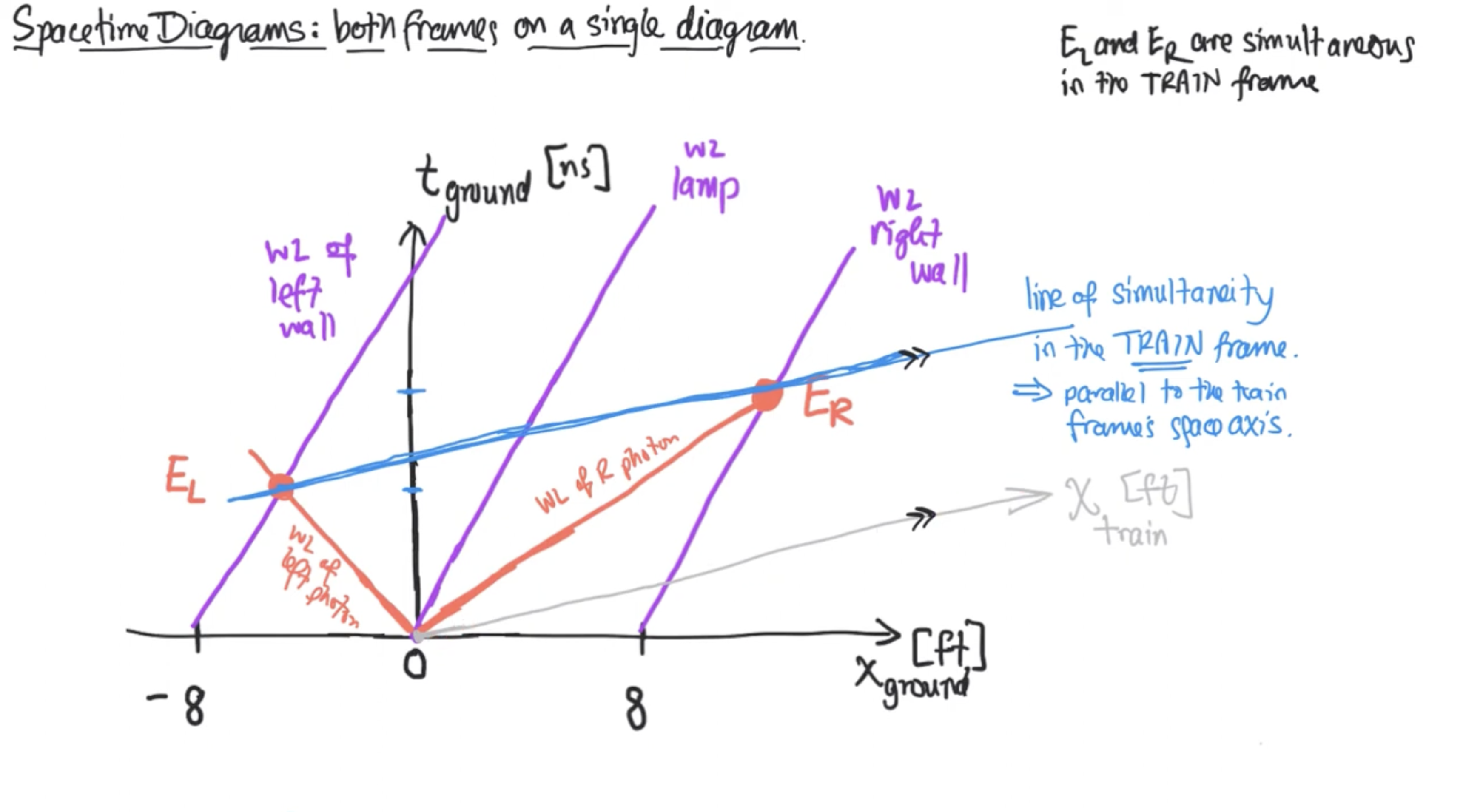
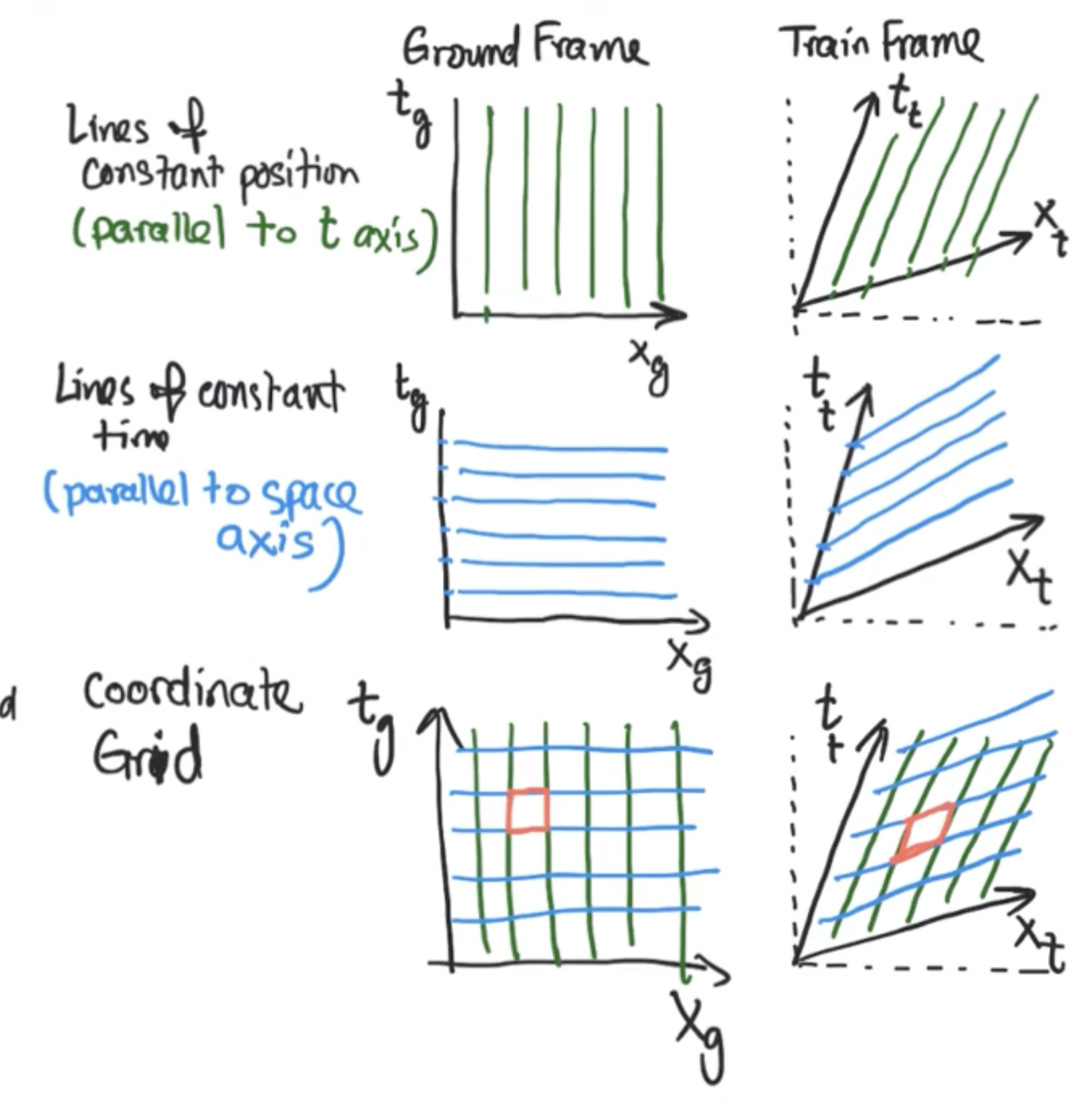
Interpreting varying inertial frames
Different inertial reference frames are just different coordinate systems used to label events in 4D Minkowski spacetime. Each frame represents a different way to “slice up” the same underlying geometry into space and time coordinates.
Think of it like drawing different sets of grid lines on the same sheet of paper. The sheet (spacetime) itself doesn’t change, but different observers choose different ways to assign coordinates to events. The Lorentz transformations are then just the rules for converting between these different coordinate systems while preserving the fundamental invariants of the geometry (like the spacetime interval).
The key invariant is the spacetime interval between any two events stays the same, like how the distance between two points on a curved 2D surface is the same regardless of what coordinate system you use to measure it1:
Note that , , , and are all different in each reference frame.
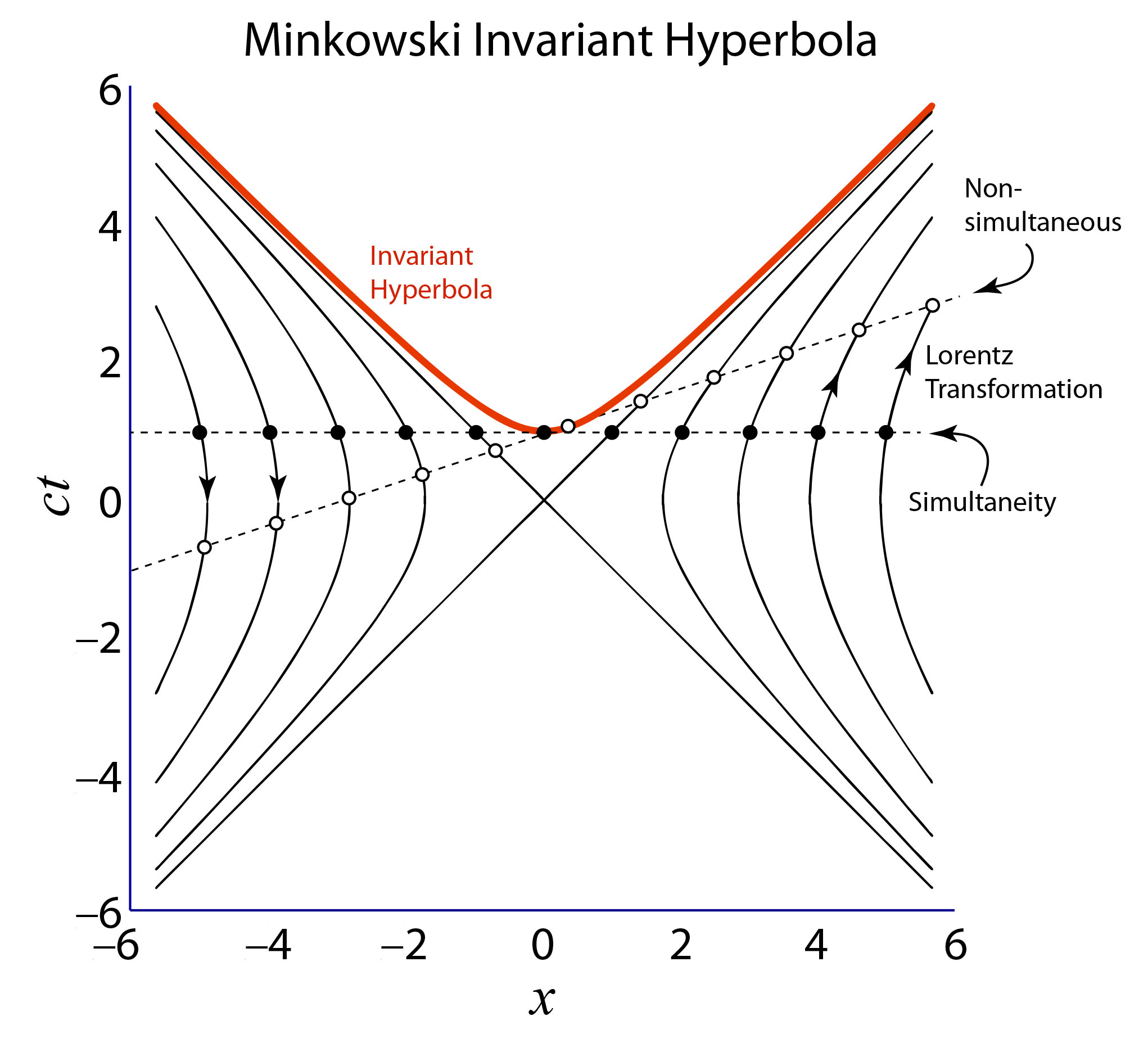
Minkowski Invariant Hyperbola
We can use the Minkowski Invariant Hyperbola to visualize how spatial distances are mapped in different frames via the Lorentz Transformation. The Lorentz transformation relates two inertial frames of reference, where an observer stationary at the event (0, 0) makes a change of velocity along the x-axis.
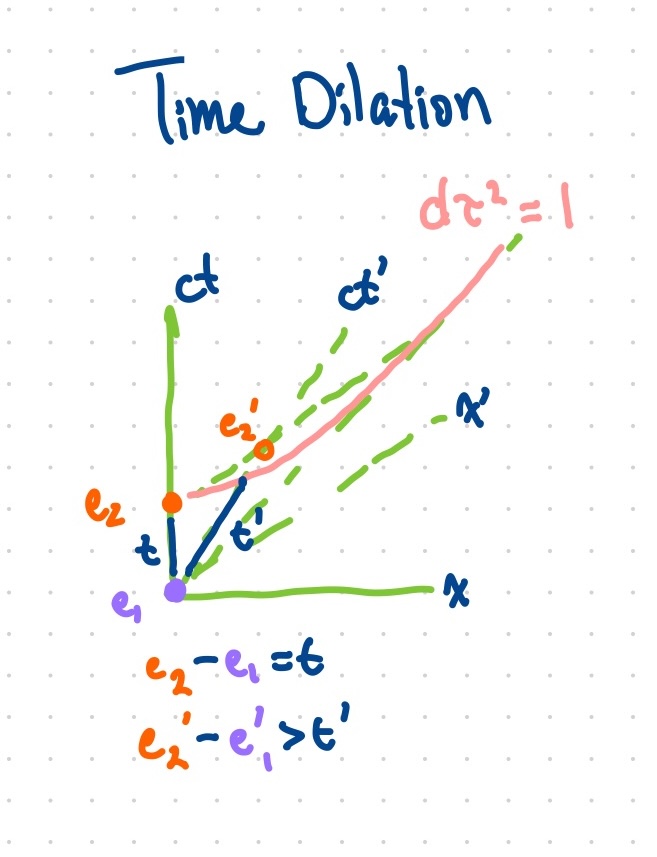
Time Dilation
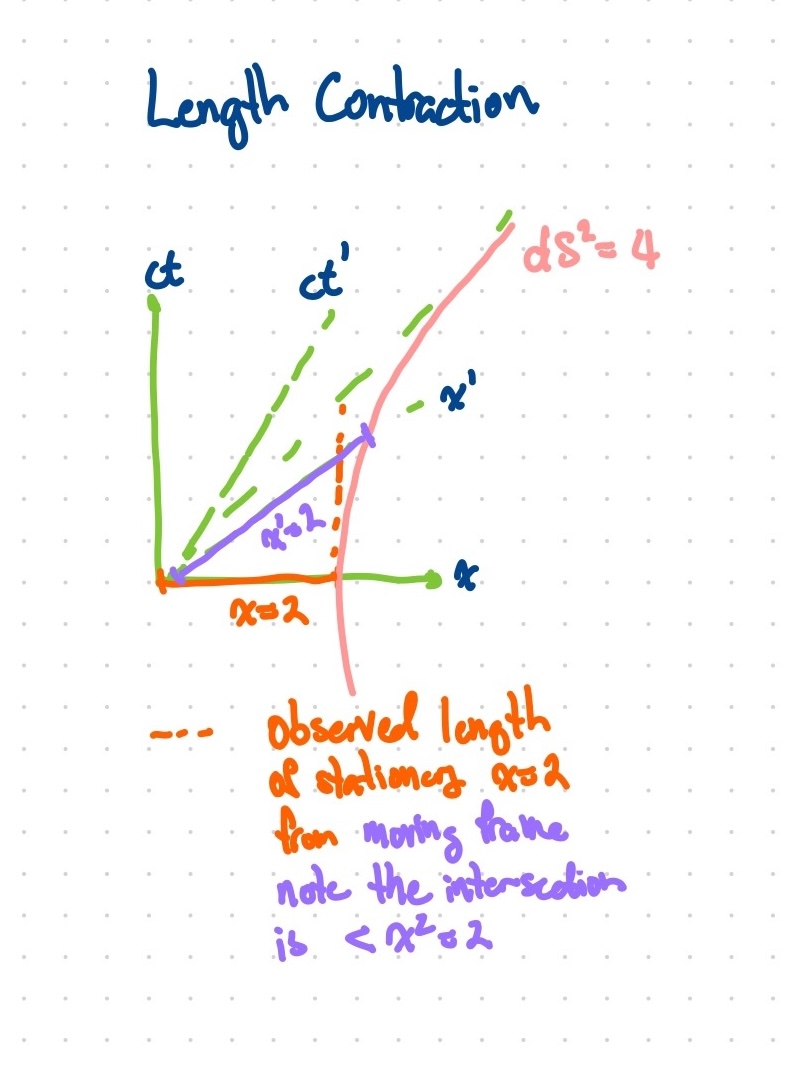
Length Contraction
Footnotes
-
Think of drawing a path on a balloon’s surface - the actual length of that path doesn’t change whether you measure it in latitude/longitude or any other coordinate system. When we transform between coordinate systems, all the mathematical terms adjust in a way that keeps the distance formula invariant. ↩